



Next: Bibliography
Up: General Configurations
Previous: Algorithm
Conversions between Positions and Connectors
In terms of the struct BONDS_GROUP
which has
![$ ({\tt np}, {\tt ip[np]}, {\tt bonds[np-1]})$](img66.png) ,
we can construct the conversions
,
we can construct the conversions
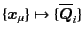 and
and
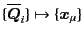 .
.
First, we see the system with a single group.
Because we only take the independent bonds,
the bond index 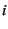 runs from 0 to
runs from 0 to 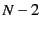 (where the number of independent bonds is
(where the number of independent bonds is 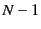 ),
while the particle index
),
while the particle index 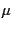 runs from 0 to
runs from 0 to 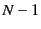 (where the number of particles is
(where the number of particles is 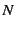 ).
Adding the
).
Adding the 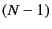 -th element of the connector vector
-th element of the connector vector
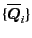 by the center of mass
by the center of mass
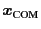 as
as
![$\displaystyle \overline{\bm{Q}}_{N-1} := \bm{x}_{\text{COM}} = \frac{1}{N} \sum_{i=0}^{N-1} \bm{x}_{{\tt ip}[i]} ,$](img72.png) |
(9.11) |
(therefore, precisely speaking,
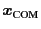 is not
the center of mass though),
the numbers of elements of both
is not
the center of mass though),
the numbers of elements of both
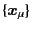 and
and
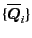 become the same.
become the same.
The transformations between them can be constructed as follows.
By definition of connector vectors,
![$\displaystyle \overline{\bm{Q}}_{i} = \bm{x}_{\alpha_{{\tt bonds}[i]}} - \bm{x}_{\beta_{{\tt bonds}[i]}} ,$](img31.png) |
(9.12) |
for
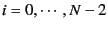 .
The last element of the connector vector
.
The last element of the connector vector
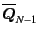 is given by
Eq. (9.11).
This is implemented in the routine BONDS_pos_to_conn_1.
Note that, for the isolated particle,
we define the (generalized) connector vector by
the position itself as
is given by
Eq. (9.11).
This is implemented in the routine BONDS_pos_to_conn_1.
Note that, for the isolated particle,
we define the (generalized) connector vector by
the position itself as
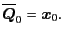 |
(9.13) |
As we see, the relation is linear and the transformation can be
expressed by
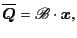 |
(9.14) |
where
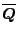 and
and 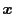 are the generalized vector
with
are the generalized vector
with 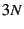 dimension for
dimension for
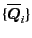 and
and
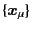 ,
respectively, and
,
respectively, and
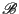 is
is
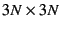 matrix based on the
matrix based on the 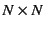 matrix
matrix
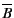 in Eq. (9.4).
in Eq. (9.4).
The opposite transformation
from
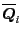 to
to
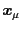 can be obtained
from the inversion matrix
can be obtained
from the inversion matrix
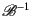 .
Alternatively (and directly),
we can calculate the position vectors from the connector vectors
(and the center-of-mass vector) as follows:
For the isolated particle,
.
Alternatively (and directly),
we can calculate the position vectors from the connector vectors
(and the center-of-mass vector) as follows:
For the isolated particle,
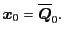 |
(9.15) |
For the group with 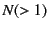 particles,
we take the two steps:
particles,
we take the two steps:
- at the first step,
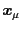 is formed
with respect to the origin at the
is formed
with respect to the origin at the
![$ \bm{x}_{\alpha_{{\tt bonds}[0]}}$](img85.png) ,
,
- then, adjust the origin
with respect to
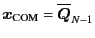 .
.
At the first step,
therefore, we define
![$\displaystyle \bm{x}_{\alpha_{{\tt bonds}[0]}} = \bm{0},$](img87.png) |
(9.16) |
as an initial condition.
After it, for the independent bond 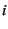 from 0 to
from 0 to 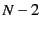 ,
,
![$\displaystyle \bm{x}_{\beta_{{\tt bonds}[i]}} = \bm{x}_{\alpha_{{\tt bonds}[i]}} - \overline{\bm{Q}}_{i} .$](img88.png) |
(9.17) |
To make this procedure work,
we should assure that
![$ \bm{x}_{\alpha_{{\tt bonds}[i]}}$](img89.png) has been defined
by the
has been defined
by the 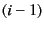 -th step.
This condition is satisfied from the fact that
-th step.
This condition is satisfied from the fact that
- bonds[] don't have redundant bonds,
- the number of the independent bond is np-1,
- the particle indices
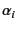 and
and 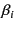 are
sorted as in Eq. (9.10),
are
sorted as in Eq. (9.10),
- bonds[] itself is sorted as
![$ {\tt bonds}[i] < {\tt bonds}[i+1]$](img91.png) .
.
After the first step,
we calculate
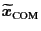 as
as
![$\displaystyle \widetilde{\bm{x}}_{\text{COM}} = \frac{1}{N} \sum_{i=0}^{N-1} \b...
...\left( = \frac{1}{N} \sum_{i=0}^{N-2} \bm{x}_{\beta_{{\tt bonds}[i]}} \right) ,$](img93.png) |
(9.18) |
and adjust the center of mass to
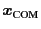 as
as
![$\displaystyle \bm{x}_{{\tt ip}[i]} = \bm{x}_{{\tt ip}[i]} - \widetilde{\bm{x}}_{\text{COM}} + \bm{x}_{\text{COM}} ,$](img94.png) |
(9.19) |
for
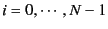 .
.
It should be noted that
the calculation of this rather tedeous procedure is 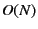 ,
while the inversion
,
while the inversion
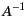 usually costs
usually costs 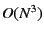 .
.
For the system containing many groups at the same time,
we can apply the above procedure for each group separately,
and the overall calculation is still 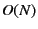 .
This system-wide transformations are implimented in the routines
BONDS_pos_to_conn and BONDS_conn_to_pos.
.
This system-wide transformations are implimented in the routines
BONDS_pos_to_conn and BONDS_conn_to_pos.




Next: Bibliography
Up: General Configurations
Previous: Algorithm
Kengo Ichiki 2008-10-12
![]() runs from 0 to
runs from 0 to ![]() (where the number of independent bonds is
(where the number of independent bonds is ![]() ),
while the particle index
),
while the particle index ![]() runs from 0 to
runs from 0 to ![]() (where the number of particles is
(where the number of particles is ![]() ).
Adding the
).
Adding the ![]() -th element of the connector vector
-th element of the connector vector
![]() by the center of mass
by the center of mass
![]() as
as
![]() to
to
![]() can be obtained
from the inversion matrix
can be obtained
from the inversion matrix
![]() .
Alternatively (and directly),
we can calculate the position vectors from the connector vectors
(and the center-of-mass vector) as follows:
For the isolated particle,
.
Alternatively (and directly),
we can calculate the position vectors from the connector vectors
(and the center-of-mass vector) as follows:
For the isolated particle,
![]() as
as
![$\displaystyle \widetilde{\bm{x}}_{\text{COM}} = \frac{1}{N} \sum_{i=0}^{N-1} \b...
...\left( = \frac{1}{N} \sum_{i=0}^{N-2} \bm{x}_{\beta_{{\tt bonds}[i]}} \right) ,$](img93.png)
![]() ,
while the inversion
,
while the inversion
![]() usually costs
usually costs ![]() .
.
![]() .
This system-wide transformations are implimented in the routines
BONDS_pos_to_conn and BONDS_conn_to_pos.
.
This system-wide transformations are implimented in the routines
BONDS_pos_to_conn and BONDS_conn_to_pos.