



Next: Question:
Up: Hydrodynamic Interaction in Stokes
Previous: Hydrodynamic Interaction in Stokes
In a viscous fluid, objects are dragged by the surrounding fluid.
(Imagine when you are in water pool or the sea.)
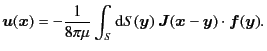 |
(3.10) |
Boundary value problem (Dirichlet problem).
Expanding the integrand in the right-hand side
of Eq. (3.10),
we have
![$\displaystyle \bm{u} (\bm{x}) = - \frac{1}{n!} \sum_{n=0}^{\infty} \frac{1}{8\p...
...t^n \int_S {\rm d}S(\bm{y})\ \Bigl[ \bm{y} - \bm{y}_0 \Bigr]^n \bm{f}(\bm{y}) ,$](img126.png) |
(3.11) |
where we assume that the surface  consists of a single sphere
and
consists of a single sphere
and  is its center.
is its center.
Note that the surface integral in the right-hand side
is a tensor of order  and
is called the force moment
and
is called the force moment

![$\displaystyle \mathcal{F}^{(n)} (\bm{y}_0) := - \int_S {\rm d}S(\bm{y})\ \Bigl[ \bm{y} - \bm{y}_0 \Bigr]^n \bm{f}(\bm{y}) ,$](img131.png) |
(3.12) |
and
Taking the terms up to  and substituting the above,
we have an expression[6]
and substituting the above,
we have an expression[6]
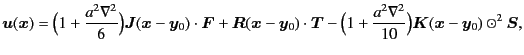 |
(3.15) |
where  and
and  are given by
are given by
Up to this order of expansion,
if we introduce the corresponding velocity moments, that is,
the translational and angular velocity  and
and
 and the rate of strain tensor
and the rate of strain tensor  ,
we have the closed linear set of equations
written in the matrix form as
,
we have the closed linear set of equations
written in the matrix form as
![$\displaystyle \left[ \begin{array}{c} \bm{U}\\ \bm{\Omega}\\ \bm{E} \end{array}...
...t] \cdot \left[ \begin{array}{c} \bm{F}\\ \bm{T}\\ \bm{S} \end{array} \right] .$](img146.png) |
(3.18) |
From the mathematical property of Eq. (3.10),
the whole matrix relating two vectors
 and
and
 should be symmetric.
That is,
should be symmetric.
That is,
However, we should note that
once we reduce the elements of vectors,
the symmetry does not hold.
From the definition, the second order tensors  and
and  are symmetric and traceless, so that only 5 components
out of
are symmetric and traceless, so that only 5 components
out of  are independent.
Without the reduction to the independent components,
the linear set of equation becomes ill-defined
and the inverse matrix (with the full components) are not unique.
are independent.
Without the reduction to the independent components,
the linear set of equation becomes ill-defined
and the inverse matrix (with the full components) are not unique.
Subsections




Next: Question:
Up: Hydrodynamic Interaction in Stokes
Previous: Hydrodynamic Interaction in Stokes
Kengo Ichiki 2008-10-12
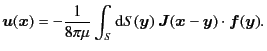
![$\displaystyle \bm{u} (\bm{x}) = - \frac{1}{n!} \sum_{n=0}^{\infty} \frac{1}{8\p...
...t^n \int_S {\rm d}S(\bm{y})\ \Bigl[ \bm{y} - \bm{y}_0 \Bigr]^n \bm{f}(\bm{y}) ,$](img126.png)
![]() and
is called the force moment
and
is called the force moment
![]()
![$\displaystyle \mathcal{F}^{(n)} (\bm{y}_0) := - \int_S {\rm d}S(\bm{y})\ \Bigl[ \bm{y} - \bm{y}_0 \Bigr]^n \bm{f}(\bm{y}) ,$](img131.png)
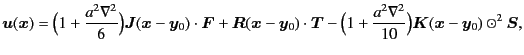
![]() and
and
![]() and the rate of strain tensor
and the rate of strain tensor ![]() ,
we have the closed linear set of equations
written in the matrix form as
,
we have the closed linear set of equations
written in the matrix form as
![]() and
and
![]() should be symmetric.
That is,
should be symmetric.
That is,